CMU 15-112: Fundamentals of Programming and Computer Science
Class Notes: Efficiency
- Big-O
- Common Function Families
- Efficiency
- The Big Idea
- Examples
- Searching
- Sorting
- sumOfSquares Examples
- Big-O
- Describes behavior of a function as the size of its input grows
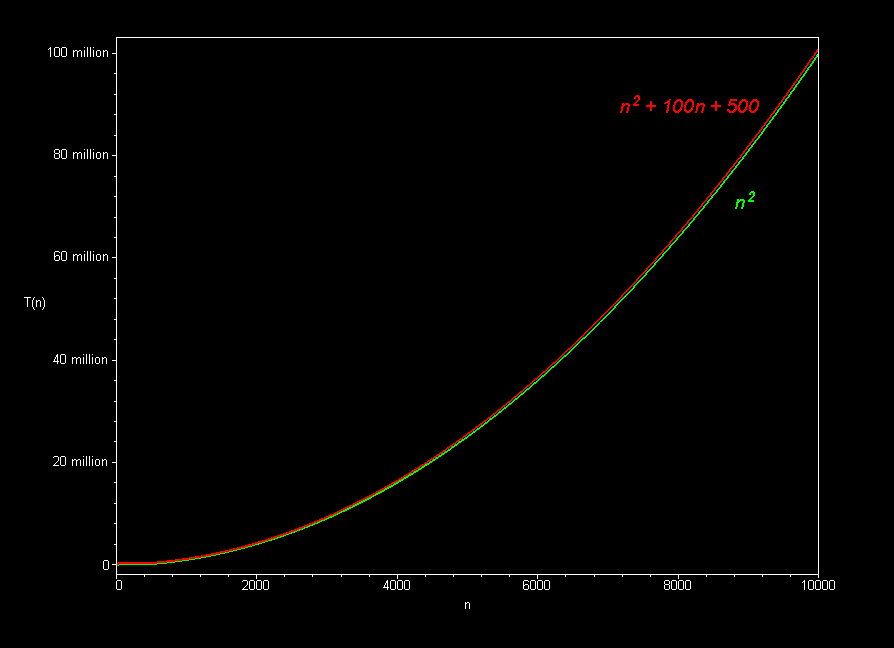
- Informally (for 15112): ignore all lower-order terms and constants
- Formally (after 15112): see here
- A few examples in math functions:
- 3n2 - 2n + 25 is O(n2)
- 30000n2 + 2n - 25 is O(n2)
- 0.00000000001n2 + 123456789n is O(n2)
- 10nlog17n + 25n - 17 is O(nlogn)
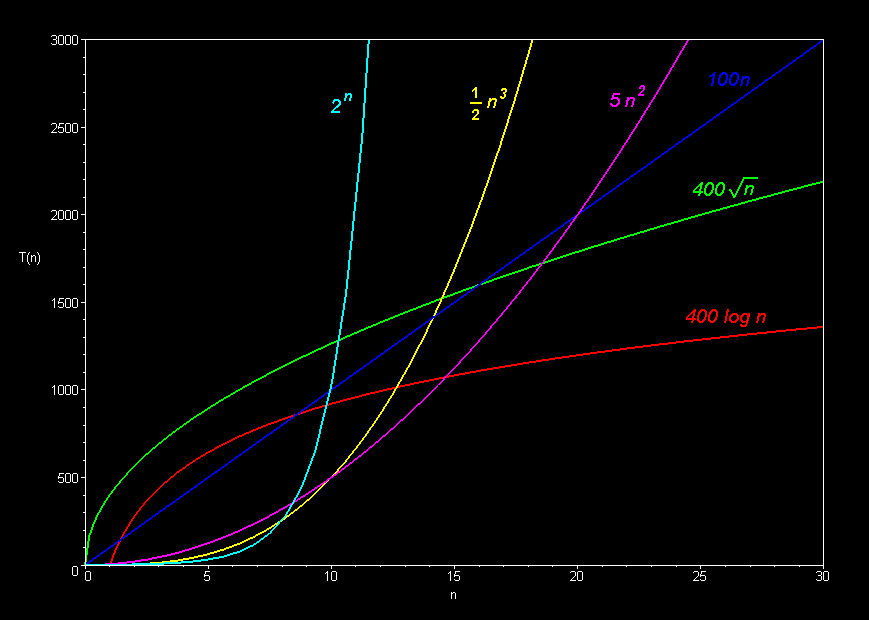
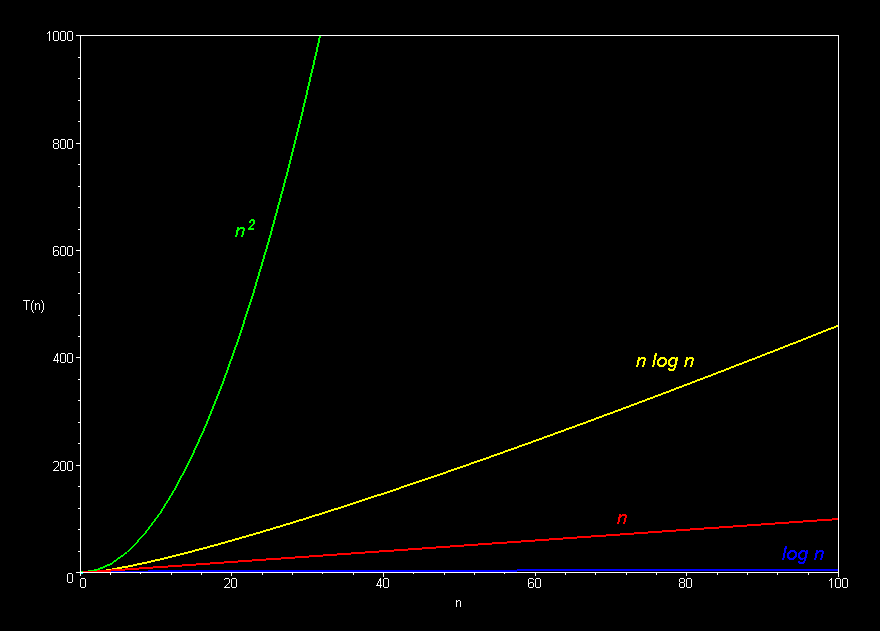
- Common Function Families
- Constant O(1)
- Logarithmic O(logn)
- Square-Root O(n0.5)
- Linear O(n)
- Linearithmic, Loglinear, or quasilinear O(nlogn)
- Quadratic O(n2)
- Exponential O(kn)
- Efficiency
When we say the program runs in O(N), we mean...- N is the size of our input
- For a string s, N = len(s)
- For a list lst, N = len(lst) (also true for sets, dictionaries, and other collections)
- For an integer n, N = n
- We can technically calculate Big-O for a number of program attributes, like time, space, bandwidth, etc. But in this class, we mainly care about time.
- For time, we usually measure algorithmic steps rather than elapsed time (These share the same Big-O, but algorithmic steps are easier to precisely describe and reason over)
- Algorithmic steps could be single lines of computation, or comparisons and swaps in a list, etc
- Can verify by timing your code's execution with: time.time()
- N is the size of our input
- Note that you can measure worst-case or average case, or even other cases such as best case (which often is trivial to compute and not very useful in practice). For 15-112, we often omit this term (which is a notable simplification that you will not see in future courses), and we nearly always mean worst-case, which is quite useful and generally easier to compute than average-case.
- The Big Idea
- Each function family grows much faster than the one before it!
- And: on modern computers, any function family is usually efficient enough on small n, so we only care about large n
- So... Constants do not matter nearly as much as function families
- Practically...
- Do not prematurely or overly optimize your code
- Instead: think algorithmically!!!
- Examples
- Sequences, Nesting, and Composition
- Sequencing
# what is the total cost here? L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N L.sort() # This is O(NlogN) L.sort(reverse=True) # This is O(NlogN) L[0] -= 5 # This is O(1) print(L.count(L[0]) + sum(L)) # This is O(N) + O(N) - Nesting
# what is the total cost here? L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N for c in L: # This loop's body is executed O(N) times L[0] += c # This is O(1) L.sort() # This is O(NlogN) print(L) # This is O(N) (why?) - Composition
# what is the total cost here? def f(L): # assume L is an arbitrary list of length N L1 = sorted(L) # This is O(NlogN) return L1 # This is O(1) def g(L): # assume L is an arbitrary list of length N L1 = L * len(L) # This is O(N**2) (why?) return L1 # This is O(1) L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N L = f(g(L)) # What is the Big-O of this? print(L) # This is O(N**2) (why?)
- Sequencing
- Sequences, Nesting, and Composition
- Python Builtins
The efficiency of the built-in functions in Python will affect the efficiency of the functions they are used in. We do not expect you to memorize the builtin efficiencies; instead, you may look them up in the table provided below when needed. We will include the relevant subset of this table on quizzes and exams.
General Function/Method Complexity Code Example Print O(N) # where N is the size of the input print(input)
Range in Iteration Number of iterations = (end - start)/step for i in range(start, end, step):...
Strings: s is a string with N characters Function/Method Complexity Code Example Len O(1) len(s)
Membership O(N) "a" in s
Get single character O(1) value = s[index]
Get slice O(end - start) s[start:end]
Get slice with step O((end - start)/step) s[start:end:step]
Chr() and Ord() O(1) chr(s) ord(s)
Concatentation O(len(s1) + len(s2)) s3 = s1 + s2
Character Type Methods O(N) s.isalnum() s.isalpha() s.isdigit() s.islower() s.isspace() s.isupper()
String Edit Methods O(N) s.lower() s.upper() s.replace() s.strip()
Substring Search Methods O(N) s.count() s.startswith() s.endswith() s.find() s.index()
Lists: L is a list with N elements Function/Method Complexity Code Example Len O(1) len(L)
Append O(1) L.append(value)
Extend O(K) # len(a) = K L.extend(a)
Concatentation with += O(K) # len(a) = K L += a
Concatentation with + O(N + K) # len(a) = K L = L + a
Membership Check O(N) item in L
Pop Last Value O(1) L.pop()
Pop Intermediate Value O(N) L.pop(index)
Count values in list O(N) L.count(item)
Insert O(N) L.insert(index, value)
Get value O(1) value = L[index]
Set value O(1) L[index] = value
Remove O(N) L.remove(value)
Get slice O(end - start) L[start:end]
Get slice with step O((end - start)/step) L[start:end:step]
Sort O(N log (N)) L.sort() sorted(L)
Multiply O(N*D) #where D is an int A = L*D
Minimum O(N) min(L)
Maximum O(N) max(L)
Copy O(N) copy.copy(L)
Deep Copy O(N*M) # where L is a 2D list with N rows and M cols copy.deepcopy(L)
Sets: s is a set with N elements Function/Method Complexity Code Example Len O(1) len(s)
Membership O(1) elem in s
Adding an Element O(1) s.add(elem)
Removing an Element O(1) s.remove(elem) s.discard(elem)
Union O(len(s) + len(t)) s|t
Intersection O(min(len(s), len(t))) s&t
Difference O(len(s)) s - t
Clear O(len(s)) s.clear()
Copy O(len(s)) s.copy()
Dictionaries: d is a dictionary with N key-value pairs Function/Method Complexity Code Example Len O(1) len(d)
Membership O(1) key in d
Get Item O(1) value = d[key] d.get(key, defaultValue)
Set Item O(1) d[key] = value
Delete Item O(1) del d[key]
Clear O(N) d.clear()
Copy O(N) d.copy()
For a more complete list, see here - Searching
- Linear search
- Basic idea: check each element in turn
- Use: find an element in an unsorted list
- Cost: O(N)
- Binary search
- Basic idea: in a sorted list, check middle element, eliminate half on each pass
- Uses:
- Find an element in a sorted list
- Number-guessing game (eg: guess a random number between 1 and 1000)
- Find a root (zero) of a function with bisection (adapted binary search)
- Cost: O(logN)
- Linear search
- Sorting
- Sorting Examples
See here. - Sorting Links
- SelectionSort vs MergeSort
- Definitions
- Selection Sort: repeatedly select largest remaining element and swap it into sorted position
- Mergesort: sort blocks of 1's into 2's, 2's into 4's, etc, on each pass merging sorted blocks into sorted larger blocks
- Analysis
This is mostly informal, and all you need to know for a 112-level analysis of these algorithms. You can easily find much more detailed and rigorous proofs on the web.- selectionsort
On the first pass, we need N compares and swaps (N-1 compares and 1 swap).
On the second pass, we need only N-1 (since one value is already sorted).
On the third pass, only N-2.
So, total steps are about 1 + 2 + ... + (N-1) + N = N(N+1)/2 = O(N2). - mergesort
On each pass, we need about 3N compares and copies (N compares, N copies down, N copies back).
So total cost = (3N steps per pass) x (# of passes)
After pass 0, we have sorted lists of size 20 (1)
After pass 1, we have sorted lists of size 21 (2)
After pass 2, we have sorted lists of size 22 (4)
After pass k, we have sorted lists of size 2k
So we need k passes, where N = 2k
So # of passes = k = log2N
Recall that total cost = (3N steps per pass) x (# of passes)
So total cost = (3N)(log2N) = O(NlogN).
Note: This is the theoretical best-possible Big-O for comparison-based sorting!
- selectionsort
- Definitions
- Sorting Examples
- sumOfSquares Examples
Note: Run this code in Standard Python, as it will timeout if you run it in brython.# The following functions all solve the same problem: # Given a non-negative integer n, return True if n is the sum # of the squares of two non-negative integers, and False otherwise. def f1(n): for x in range(n+1): for y in range(n+1): if (x**2 + y**2 == n): return True return False def f2(n): for x in range(n+1): for y in range(x,n+1): if (x**2 + y**2 == n): return True return False def f3(n): xmax = int(n**0.5) for x in range(xmax+1): for y in range(x,n+1): if (x**2 + y**2 == n): return True return False def f4(n): xyMax = int(n**0.5) for x in range(xyMax+1): for y in range(x,xyMax+1): if (x**2 + y**2 == n): return True return False def f5(n): xyMax = int(n**0.5) for x in range(xyMax+1): y = int((n - x**2)**0.5) if (x**2 + y**2 == n): return True return False def testFunctionsMatch(maxToCheck): # first, verify that all 5 functions work the same print("Verifying that all functions work the same...") for n in range(maxToCheck): assert(f1(n) == f2(n) == f3(n) == f4(n) == f5(n)) print("All functions match up to n =", maxToCheck) testFunctionsMatch(100) # use larger number to be more confident import time def timeFnCall(f, n): # call f(n) and return time in ms # Actually, since one call may require less than 1 ms, # we'll keep calling until we get at least 1 secs, # then divide by # of calls we had to make calls = 0 start = end = time.time() while (end - start < 1): f(n) calls += 1 end = time.time() return float(end - start)/calls*1000 #(convert to ms) def timeFnCalls(n): print("***************") for f in [f1, f2, f3, f4, f5]: print ("%s(%d) takes %8.3f milliseconds" % (f.__name__, n, timeFnCall(f, n))) timeFnCalls(1001) # use larger number, say 3000, to get more accurate timing
Graphically (Images borrowed from here):