CMUQ 15-121 Hash Tables
1. Introduction
In this set of notes we’ll talk about hash tables, an unordered data structure designed to allow for extremely fast add and find. Although the theoretical worst case efficiency of the hash table presented here will be \(O(N)\), in practice hash tables are much closer to \(O(1)\).
A hash table is a data structure that stores items, unordered, into an array in such a way that adding new items and finding existing items is extremely fast. This should immediately make you suspicious: If the items are stored unordered, then how is it possible to find an item quickly? Didn’t we previously establish that finding an item in an unordered array requires a linear search, and is therefore \(O(N)\)? We did, but with a simple trick a hash table can overcome this.
2. Hash Function
A hash function is a mathematical operation that takes an item and reduces it to a number. A good hash function has the following properties:
- The hash function must always returns the same number when given the same item.
- For example, if the string “John Smith” hashes to 12432, then that same string should always hash to 12432.
- The hash function should produce a uniform distribution of values.
- This means that, roughly, speaking, if you hash 1,000,000 different items, you should not get that many items that have the same hash.
In Java, objects provided by the Java API provide their own hash functions in the hashCode() method. You can call .hashCode() on most objects and it will return an integer that is the hash of that object. If you write your own object, then you should provide your own hashCode() method. (More on this later.)
3. Hash Table
Now that we’ve discussed a hash function, we can describe a hash table. A hash table uses a hash function to quickly distribute items into an array of a fixed size. We call each element of the array a bucket. The concept is simple: When you want to add an item to a hash table, you calculate its hash value and put it into the bucket that corresponds to that hash value. Consider the following example of hashing strings:
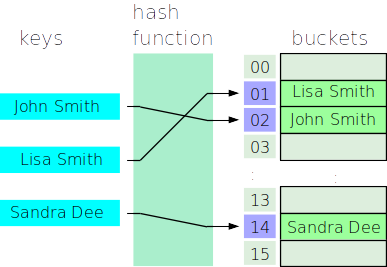
In this example we have a hash function capable of mapping a string to an integer in the range 0 to 15. (If your hash function just produces any integer, then you use the modulo operator (% 16) to bring the number into the range 0 to 15.) The hash value of a string determines which bucket it gets stored in.
If we later want to determine if an item is in the table, we hash the item and check its bucket to see if it is there.
The efficiency of this is extremely good. Assuming your hash function is \(O(1)\), then adding and searching in the table are both \(O(1)\). That’s actually amazing!
Of course, this isn’t without complications.
3.1. Collisions
As presented so far, hash tables seem wonderful. Constant time adding and finding. There is one situation that we haven’t discussed yet, however, which is collisions. A collision is when two items in the hash table have the same hash.
3.1.1. Collision Example
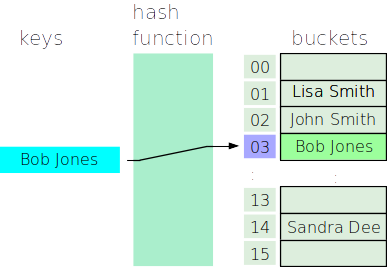
- Consider the following hash table with 3 items in it:

- Let’s say we want to add “Bob Jones” to the table, and “Bob Jones” hashes to 3:
- Now we want to add another entry, “Tamim AlMarri”, which hashes to 1. There is a problem, however. There is already an item at location 1:
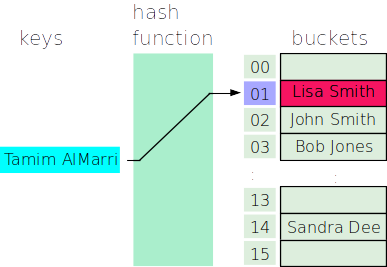
This is almost certain to happen eventually (just playing the odds), so we need to be able to handle it. So, what do we do? There are a variety of approaches to handling this situation, but we’ll discuss the one that is both simplest and most commonly used: Just store a list of items at the bucket, like so:

3.1.2. Changing Add and Find
This slightly complicates our add and find operations, but not by much. When adding, we need to add them item to the list if the bucket isn’t empty. When doing find, we need to search the entire list at the bucket.
3.1.3. Efficiency Analysis
With this new change, our efficiency analysis changes as well. Let’s imagine the worst case scenario for a hash table that handles collisions using a list. In the absolute worst case, all items have the same hash and are stored in the same bucket. Like so:
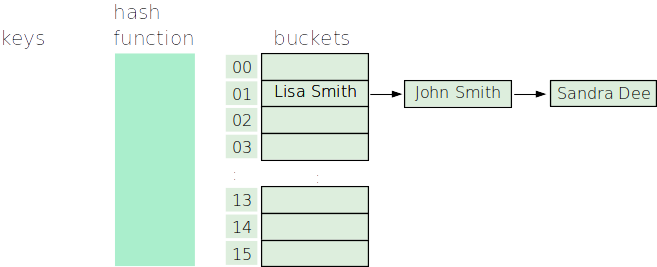
If this happens:
- Adding is still \(O(1)\). If you imagine it as a linked list at the bucket, then you can just add the new item at the head.
- Finding is now \(O(N)\). Since all the items are simply in a linked list, finding one of them is \(O(N)\). (Note: You could improve this by storing a tree at each bucket, but for now let’s keep things simple.)
This is the absolute worst case, and it shouldn’t happen if your hash function provides a uniform distribution. Instead, those items will be spread throughout the table.
3.1.4. Minimizing Collisions
The more collisions you have, the worse the performance of the hash table becomes. Assuming you have a good hash function, the property of the table that most impacts collisions is the size of the table. To understand this, let’s think about the extremes:
- Imagine you create a hash table with 2 buckets and you add 1,000,000 items to it. Even with a good hash function, there would be lots of collisions and roughly 500,000 items per bucket. This would perform horribly, because adding and finding would requiring linear searching 500,000 items. You would never want to do this.
- Now imagine you create a hash table with 1,000,000,000 buckets and you add 1,000,000 items to it. The chances of a collision are extremely low, and this will perform amazingly. It will waste a lot of space, however, so you wouldn’t really want to do this, either.
Therefore, you need to find the “sweet spot” for the size of the hash table vs. the number of items you plan to put into it. So what is ideal? It depends on your workload. Some random people on the Internet indicate that you should probably have 1.3x the number of items you plan to store. Your mileage may vary.
3.2. Limitations
There are a number of limitations of hash tables:
- Wasted space. Your hash table needs to be large enough to minimize collisions, which may mean wasted space. You should also have some idea of how many items you plan to put into it in order to balance this.
- No order. Items in a hash table are ordered by their hash value, which isn’t an order than makes any sense to people. If you want to traverse the contents in order, then a hash table isn’t a good choice.
4. Hash Codes
In Java, most objects implement their own hash function suitable for calculating their hash. This is the hashCode method. If you write your own object, it will include a default hashCode method that will work just fine.
However, if your object provides a custom compareTo() method and/or an equals() method, then you must provide your own hashCode method that is consistent with them. In this case, consistent means that if compareTo() and equals() say that two objects are equal, then their hashes must be the same as well. In practice, this usually just means generating an object’s hash codes based on the hash codes of its attributes.
For some examples of implementing your own hash codes, try this website.
5. Image Credits
The images in this set of notes are a modified version of this one by Jorge Stolfi and hosted by Wikimedia. The original, and these modified versions, are available under the Creative Commons Attribution-Share Alike 3.0 Unported license.