CMUQ 15-121 Binary Search Trees
- 1. Introduction
- 2. Trees by Example
- 3. Binary Search Trees
- 4. Operations on a BST
- 5. Traversing a Binary Tree
- 6. Building a BST in Java
1. Introduction
In this set of notes we’ll talk about binary search trees: A data structure used to store and find sorted data quickly. Trees are the basis for a large number of other data structures, especially in databases.
2. Trees by Example
Before we talk about BSTs, let’s talk about trees in general by looking at an example:
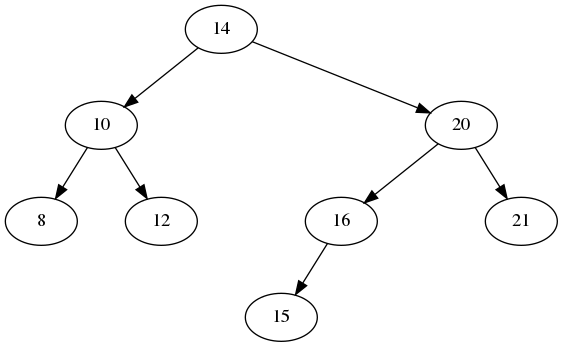
Here is some important terminology about trees in general:
- The first node is called the root of the tree.
- Example: 14 is the root in this tree.
- Each node can have children.
- Example: 8 and 12 are the children of 10.
- Each node has exactly one parent (except the root).
- Example: 10 is the parent of 8 and 12.
- A node with no children is called a leaf node.
- Example: 8, 12, 15, and 21 are all leaf nodes.
- A node that is not the root or a leaf is called an internal node.
- Example: 10, 16, and 20 are internal nodes.
- A subtree is a tree formed by a node and all of its descendants.
- Example: We could form a subtree that uses 20 as the root.
- The link between a parent and a child is called an edge.
- A path is a sequence of nodes that you can traverse to get from a higher-level node to a lower-level node. Usually you discuss paths in terms of paths from the root to a leaf.
- Example, the path from 14 to 15 is: 14 -> 20 -> 16 -> 15.
- The depth or level of a node is the length of the path from the root to that node. The root is always at level 0.
- Example: 14 has a depth of 0. 20 has a depth of 1. 15 has a depth of 3.
- The height of a tree is the maximum depth of any node in the tree. The height of a single-node tree is 0.
- Example: The height of this tree is 3, because that is the longest path in the tree.
3. Binary Search Trees
There are a few more properties that are specific to binary search trees:
- A node can have at most 2 children: left and right.
- The left subtree of a node always contains values less than the node.
- The right subtree of a node always contains values greater than the node.
Take a moment now to look again at those last two points and look at the example tree. Make sure you can see that this is true before you move on.
4. Operations on a BST
Let’s look at some common operations on a BST.
4.1. Add
If you want to add a node to the tree, you simply “walk” going left and right until you find an empty left or right pointer in the correct position. Let’s do an example.
Imagine you want to add 18 to this tree. Here is the process:
- Start at the root.
- Is 18 greater than or less than 14? Since it is greater than 14, we move to the right.
- Now we are at node 20.
- Is 18 greater than or less than 20? Since it is less than 20, we move to the left.
- Now are at node 16.
- Is 18 greater or less than 16? Since it is greater than 16, we move to the right.
- Wait! there is no node to the right of 16. That means our new node will go here. So we create a new node with 18 and make it the right child of 16.
After this process, the tree will look like:
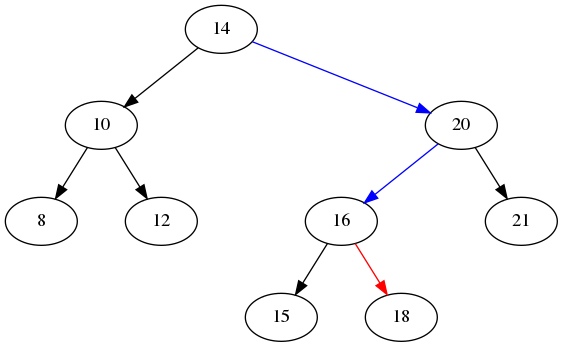
Blue represents the edges we followed while figuring where to put the new node. Red represents the new edge.
4.2. Find
If you want to find a node in the tree, you perform the same basic walk as with adding. The difference is that at the end of the walk you either find the node you are looking for or you find a null-pointer indicating it isn’t there. Let’s work two examples.
4.2.1. Find 15
- Start at the root.
- Is this node 15? No.
- Is 15 greater or less than 14? Greater, so we go right.
- Move to 20.
- Is this node 15? No.
- Is 15 greater or less than 20? Less, so we go left.
- Move to 16.
- Is this node 15? No.
- Is 15 greater or less than 16? Less, so we go left.
- Move to 15.
- Is this node 15? Yes! We found it.
Here is a graph showing the path we took:
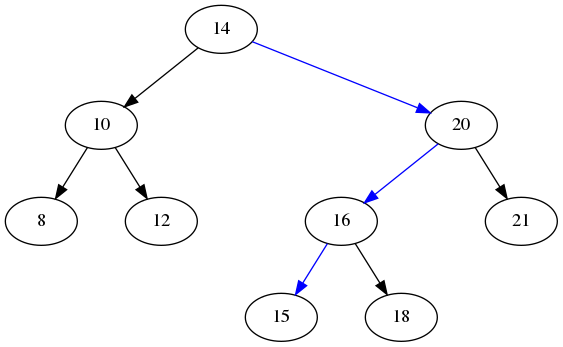
4.2.2. Find 13
- Start at the root.
- Is this node 13? No.
- Is 13 greater or less than 14? Less, so we go left.
- Move to 10.
- Is this node 13? No.
- Is 13 greater or less than 10? Greater, so we go right.
- Move to 12.
- Is this node 13? No.
- Is 13 greater or less than 12? Greater, so we go right.
- Wait! there is no right. So the node is not in the tree.
Here is a graph showing the path we took:
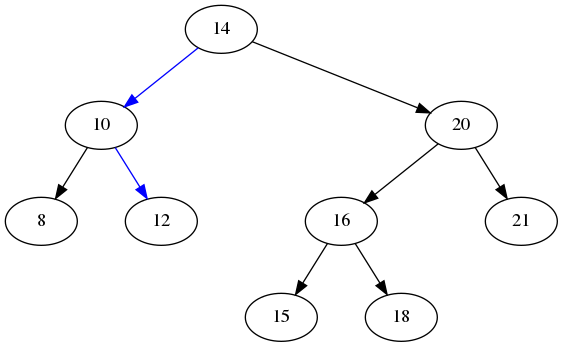
4.3. Remove
Removing a node from a BST is more complicated that adding or finding because we may need to rearrange other nodes from the tree when we do a removal. There are three scenarios for removal.
For the examples below, let’s start with the following tree:
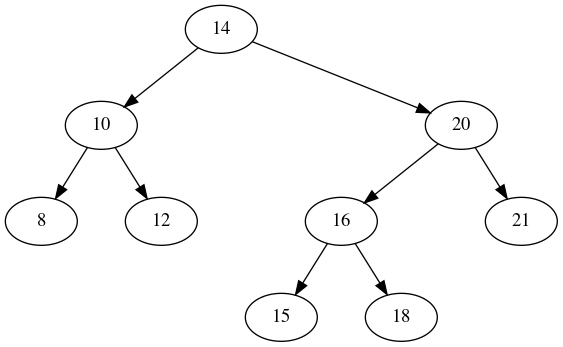
4.3.1. Removing a Node with No Children
Let’s start with a simple case: Removing node 21. If you look at the tree above, you’ll notice that 21 has no children. That makes removal of it easy: We simply remove it from the tree. In that case, our new tree would look like this:
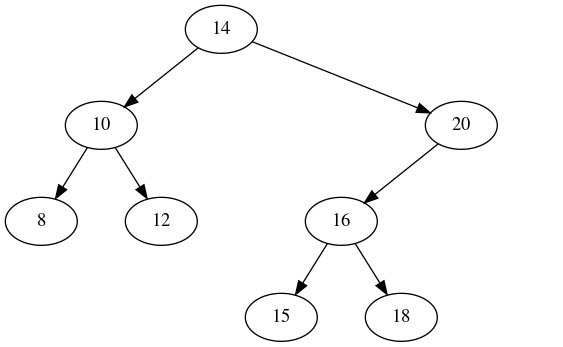
4.3.2. Removing a Node with One Child
Let’s try something more complicated: let’s remove node 20. Looking at the tree as we left it, node 20 has exactly one child. In order to get rid of it, we remove it from the tree and promote its child to its place. So, node 20 will be removed and node 16 will take its place in tree. After removing node 20, our tree will look like:
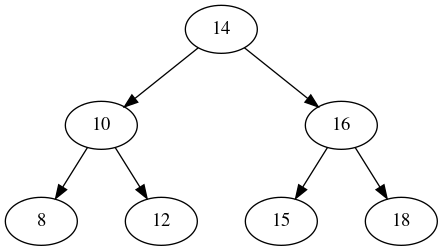
4.3.3. Removing a Node with Two Children
Now let’s move on to the hardest case: let’s remove node 14. Looking at the tree, this is more complicated because node 14 has two children, and so do its children. That means we can’t promote one of the children up.
One strategy to handle this is to find node 14’s in-order successor, which is a fancy way of saying the next node in the ordered list of nodes. Another way to the think of the in-order successor is as the left most node that is to the right of 14. (Go right from 14, then find the left-most node.) In this case, 15 is next node in order.
Because it is the left most node on the right, by definition it will either have 0 or 1 children. (The reason for this is that if it had two children, then there is a node to its left, so it isn’t the left-most node.)
So, in this scenario, we can remove 14 by replacing it with 15 and then removing 15. That makes our final tree look like:
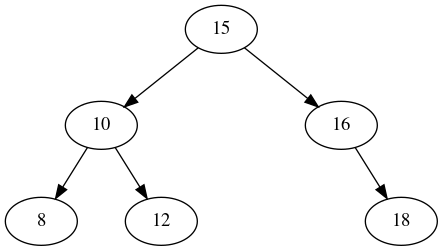
5. Traversing a Binary Tree
When you need to traverse every node in a binary tree there are three general, recursive approaches: in-order, pre-order, and post-order. These are all examples of depth first searches.
In the examples below, we’ll use the function processNode as a placeholder for whatever operation you want to perform on each node of the tree.
5.1. In-Order Traversal
When you want to traverse every node and access them in-order, you would use an algorithm that looks something like:
public void traverseInOrder(TreeNode n) {
if (n == null) {
return
}
traverseInOrder(n.left);
processNode(n);
traverseInOrder(n.right);
}
Notice that this processes everyone to the left of n, then n itself, then everyone to the right of n. This type of traversal is useful for printing the contents of the list in-order. (So, if instead of calling processNode you called print, this would print all the nodes in order.)
5.2. Pre-Order Traversal
When you want to traverse every node, but access each node immediately as it is reached, you would use an algorithm that looks something like:
public void traverseInOrder(TreeNode n) {
if (n == null) {
return
}
processNode(n);
traverseInOrder(n.left);
traverseInOrder(n.right);
}
Notice that here we process n first, then go left, then go right. This is useful if you are doing something like cloning a tree. (Because you will need to create a copy of the current node before processing its children.)
5.3. Post-Order Traversal
When you want to traverse every node, but access each node after you have processes all of its children, you would use an algorithm that looks something like:
public void traverseInOrder(TreeNode n) {
if (n == null) {
return
}
traverseInOrder(n.left);
traverseInOrder(n.right);
processNode(n);
}
This is useful for doing something like deleting all the nodes in a tree, because you need to delete all the children before deleting the node itself. It would also be useful for determining the size of a tree, because you need to count all the children, then add yourself, before returning.
6. Building a BST in Java
We’ll implement a BST in class, and you can see an example of an implementation there. The goal of these notes is simply to provide you with an overview of the concept of a binary search tree.