Homework 2

Due Tuesday 7-Sep, at 10:00pm

To start

  1. Create a folder named ‘hw2’
  2. Download hw2.py to that folder
  3. Edit hw2.py and modify the functions as required
  4. When you have completed and fully tested hw2, submit hw2.py to Gradescope. For this hw, you may submit up to 20 times (which is way more than you should require), but only your last submission counts.

Some important notes

  1. This homework is solo. You may not collaborate or discuss it with anyone outside of the course, and your options for discussing with other students currently taking the course are limited. See the academic honesty policy for more details.
  2. After you submit to Gradescope, make sure you check your score. If you aren’t sure how to do this, then ask a CA or Professor.
  3. There is no partial credit on Gradescope testcases. Your Gradescope score is your Gradescope score.
  4. Read the last bullet point again. Seriously, we won’t go back later and increase your Gradescope score for any reason. Even if you worked really hard and it was only a minor error…
  5. Do not hardcode the test cases in your solutions.
  6. The starter hw2.py file includes test functions to help you test on your own before you submit to Gradescope. When you run your file, problems will be tested in order. If you wish to temporarily bypass specific tests (say, because you have not yet completed some functions), you can comment out individual test function calls at the bottom of your file in main(). However, be sure to uncomment and test everything together before you submit! Ask a CA if you need help with this.
  7. Remember the course’s academic integrity policy. Solving the homework yourself is your best preparation for exams and quizzes; cheating or short-cutting your learning process in order to improve your homework score will actually hurt your course grade long-term.
  8. Do not use string indexing, loops, lists, list indexing, or recursion this week. The autograder will reject your submission entirely if you do.

Problems

  1. Breaking the ice on Piazza [5 pts]
    This task is easy-peasy. Make a post on Piazza asking a valid question about this homework OR answering one of questions posted by other students about this homework. Make sure your post is public and that it follows the academic integrity policy.

  2. isEvenPositiveInt(n) [5 pts]
    Write the function isEvenPositiveInt(n) which, given a value n, returns True if it is even, positive, and an integer, and False otherwise.

  3. hotdogPurchase(numHotdogs) [10 pts]
    Hot dogs are an American tradition. Each year, Americans eat up to 20 Billion hot dogs. A classic hot dog is made up of two components: A frank (the meat) and a bun. Yet, for reasons that mystify mankind, the franks are typically sold in packs of ten and the buns in packs of eight. And, of course, you must buy full packages. Write the function hotdogPurchase(numHotdogs) that takes the total number of hot dogs you want to make, and returns the number of packages of franks and the number of packages of buns you need to purchase. You may assume that the argument, numHotdogs, is a non-negative int and the function returns as ints the smallest number of packages of franks and buns that must be purchased.

    For example:
      hotdogPurchase(50) returns 5, 7. (Meaning 5 packs of franks and 7 packs of buns.)

  4. hotdogExcess(numHotdogs) [10 pts]
    Write the function hotdogExcess(numHotdogs) that takes the total number of hot dogs you want to make (as a non-negative integer) and returns the number of excess franks and buns you will need to purchase. Hint: you may want to use hotDogPurchase, which you just wrote!

    For example:
      hotdogExcess(50) returns 0, 6.

  5. playGuessingGame() [10 pts]
    Write the function playGuessingGame() which runs a short guessing game with the user. The program should ask the user two Yes-or-No questions, then guess what the user is thinking based on their answers. You must use the specific prompts shown in the example exchanges below to pass the test cases (where the bolded words are user input), so you should copy the prompts directly into your code to avoid typos.

    Let's play a guessing game! Think of a type of pet. Does it have fur?Yes Can you teach it to play fetch?Yes It's a dog!
    Let's play a guessing game! Think of a type of pet. Does it have fur?Yes Can you teach it to play fetch?No It's a cat!
    Let's play a guessing game! Think of a type of pet. Does it have fur?No Can it swim?Yes It's a fish!
    Let's play a guessing game! Think of a type of pet. Does it have fur?No Can it swim?No It's a bird!

    Hint 1: For this problem, instead of using parameters and return, you'll want to use input() and print().

    Hint 2: Make sure that you don't leave any trailing whitespace after the prompts or responses. This will mess up the autograder.

  6. nearestBusStop(street) [10 pts]
    Write the function nearestBusStop(street) that takes a non-negative int street number, and returns the nearest bus stop to the given street, where buses stop every 8th street, including street 0, and ties go to the lower street, so the nearest bus stop to 12th street is 8th street, and the nearest bus stop to 13 street is 16th street. The function returns an integer, so for example, nearestBusStop(5) returns 8.

  7. getInRange(x, bound1, bound2) [10 pts]
    Write the function getInRange(x, bound1, bound2) which takes 3 int or float values -- x, bound1, and bound2, where bound1 is not necessarily less than bound2. If x is between the two bounds, just return it unmodified. Otherwise, if x is less than the lower bound, return the lower bound, or if x is greater than the upper bound, return the upper bound. For example:
    • getInRange(1, 3, 5) returns 3 (the lower bound, since 1 lies to the left of the range [3,5])
    • getInRange(4, 3, 5) returns 4 (the original value, since 4 is in the range [3,5])
    • getInRange(6, 3, 5) returns 5 (the upper bound, since 6 lies to the right of the range [3,5])
    • getInRange(6, 5, 3) also returns 5 (the upper bound, since 6 lies to the right of the range [3,5])

  8. isPerfectCube(n) [15 pts]
    Write the function isPerfectCube(n) that takes a possibly-non-int value, and returns True if it is an int that is a perfect cube (that is, if there exists an integer m such that m**3 == n), and False otherwise. Do not crash on non-ints nor on negative ints.

  9. colorHarmony(rgb1, rgb2) [25 pts]
    In this problem you will find a color that is in "harmony" with two other colors.

    Background

    Color theory can be used to determine what colors look nice together. This is useful in many areas, including CS, where it can be applied to the design of graphical user interfaces. The color wheel was invented in the 17th century by Sir Isaac Newton, who mapped the color spectrum onto a circle. The color wheel is the basis of color theory, because it shows the relationship between colors.

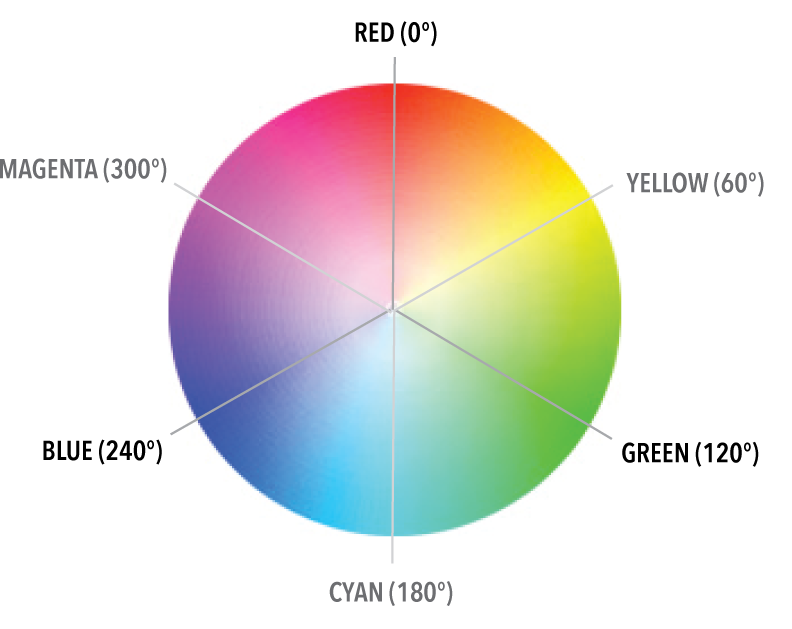
    The Color Wheel


    On computers, there are multiple ways that colors are represented. One of the earliest, and simplest, ways is called RGB. An RGB representation of a color contain 3 integers, each between 0 and 255, representing the amount of red, green, and blue respectively in the given color, where 255 is "entirely on" and 0 is "entirely off".

    A different way to represent colors is called HSV (Hue, Saturation, Value). In the HSV model, the color is mapped to the color wheel shown above, and the hue is the angle of where the color is, and saturation and value represent how "intense" the color looks. (Saturation and value aren't important for this assignment.) Given that the color wheel is a circle, the hue ranges from 0 to 360: 0 is red, 45 is a shade of orange, 55 is a shade of yellow, etc.

    Color Harmonies

    Colors that look good together are called a color harmony. Artists and designers use these to create a particular look or feel. You can use the color wheel above to find color harmonies by using a variety of rules. Color harmonies determine the relative positions of different colors in order to find colors that create a pleasing effect.

    In this task we will use the color wheel to find a color harmony based on the isosceles triad: a set of three colors that form an isosceles or -- even better -- an equilateral triangle.

    Given two colors c1, c2, your task is to determine a third color c3 that forms an isosceles triad, with the segment c1c2 being the base of the triangle. For example, consider the case where we pick two random colors on a color wheel:

    Two random colors highlighted on a color wheel

    In this case, we've picked a shade of red (RGB: 255, 38, 0) and a shade of green (RGB: 0, 255, 34). The color that is in triadic harmony with this two is the one that completes an isosceles triangle with them on the color wheel, like so:

    Two random colors highlighted on a color wheel

    That third color ends up being a shade of blue (RGB: 36, 0, 255)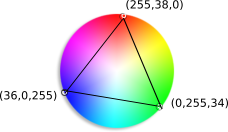

    You can imagine how that same process (finding the color that completes the triangle) could be followed for any two colors on the color wheel.

    Calculating That Third Point

    So, given the RGB values for two colors, how do you find the third color in the triangle? The process is fairly straightforward:
    1. Determine the hue value (angle) of each of the two colors. In our example above, the red color has a hue value of 9 degrees and the green color has a hue value of 128 degrees. (Go look at the first color wheel in this problem, find those angles, and convince yourself this is true.)
    2. Base on those two angles, we can find the angle of the color (the hue) that is directly across from the midpoint between the two colors. (The formula for this is left as an exercise for the reader.) Note that it could be argued there are two different points that solve the problem (one triangle going each direction from the midpoint), but we are only concerned with the one that produces the larger triangle.
    3. We can convert the hue value of the third color into RGB values.


    A Few More Things

    • For the arguments and return value to/from this function, we need to represent RGB values as a single integer. To do that, we'll use the first 3 digits for red, the next 3 for green, the last 3 for blue, all in base 10 (decimal, as you are accustomed to). Hence, we'll represent crimson as the integer 220020060, and mint as the integer 189252201. You will need to "extract" the individual red, green, and blue values from this integer.
    • You can convert colors between RGB and HSV using the formulas found here and here.
    • In order to simplify your task, we are going to consider only the colors that lie at the perimeter of the wheel. Note that, in the RGB representation of these colors, at least one of the R, G, or B components is entirely on (you can notice the "ff" in the hex representation), and at least one component is entirely off. This also means that the third color must also lie at the perimeter of the wheel.
    • Colors that lie at the perimeter have maximal saturation and value (S=100% and V=100%), so you can fix the values of S and V in any formulas.


    Your Task

    With all that in mind, write the function colorHarmony(rgb1, rgb2), which takes two integers representing colors at the perimeter of the wheel encoded as just described and returns the color in the wheel that forms a triadic harmony with those two colors.

    For example, following the case above: colorHarmony(255038000, 255034) returns 36000255 (note that 36000255 is the same integer value as 036000255, and the leading zeros is just an output formatting choice that we make when printing the value)

    To solve the task, first find the angles at which the given RGB color lie, then compute a third angle that corresponds to the RGB color that completes the isosceles triad. Lastly, convert the computed angle to the RGB color and that's your answer. If no such color exists, return None. If there are multiple solutions, return the solution with the smallest integer value..

    To do this, you must write two helper functions:
    • rgbToAngle(rgb) to find the angle at which the RGB color lies.
      • This function takes an integer that encodes the RGB color as explained above and returns the angle a, in degrees, 0 <= a < 360, at which the color lies. For simplicity, the returned angle should be integer. If the color does not lie at the perimeter, or the rgb value is invalid, the function should return None.

    • angleToRGB(a) to convert the angle to the RGB color.
      • This function takes one float value representing an angle in degrees and returns an integer that represents the RGB color.

    You may write other helper functions if you think they would be useful, but you must at least write these two exactly as described, and then you must use them appropriately in your solution. Once you have written and tested your helper functions, then move on to writing your colorHarmony function, which of course should use your helper functions. That's the whole point of helper functions. They help!

    Note that helper functions help in several ways. First, they are logically simpler; they break down your logic into smaller chunks that are easier to reason over. Second, they are independently testable, so you can more easily isolate and fix bugs. And third, they are reusable, so you can use them as helper functions for other functions in the future. All good things!