Homework 5

Due Tuesday 5-Oct, at 10pm

To start

  1. Create a folder named ‘hw5’
  2. Create a new file, hw5.py, in that folder.
  3. Edit hw5.py and add the functions as required
  4. When you have completed and fully tested hw5, submit hw5.py to Gradescope. For this hw, you may submit up to 15 times, but only your last submission counts.
  5. Note that the autograder for this assignment is more complex than many past assignments, and may require five minutes to finish autograding your submission.

Note: We have a few sample license plates you can test with. You can find them here.

Some important notes

  1. This homework is solo. You may not collaborate or discuss it with anyone outside of the course, and your options for discussing with other students currently taking the course are limited. See the academic honesty policy for more details.
  2. After you submit to Gradescope, make sure you check your score. If you aren’t sure how to do this, then ask a CA or Professor.
  3. There is no partial credit on Gradescope testcases. Your Gradescope score is your Gradescope score.
  4. Read the last bullet point again. Seriously, we won’t go back later and increase your Gradescope score for any reason. Even if you worked really hard and it was only a minor error…
  5. Do not hardcode the test cases in your solutions.
  6. We are not giving you any starter code this week. That means you need to create your file from scratch and include your own testcases. For writing testcases, follow the style of testcases uses in the previous homeworks.
  7. Remember the course’s academic integrity policy. Solving the homework yourself is your best preparation for exams and quizzes; cheating or short-cutting your learning process in order to improve your homework score will actually hurt your course grade long-term.

Limitations

Do not use sets, dictionaries, try/except, classes, or recursion this week. The autograder will reject your submission entirely if you do.

Image Processing

This programming homework is designed to get you more practice with processing images and applying the skills you have learned to solve real world problems.

Cops!

As traffic accidents increase due to over speeding and other traffic violations, it becomes important for law enforcement agencies to find technological solutions to detect these violations. In Qatar, the government has placed high resolution cameras on various roads and highways that detect speeding motorists and take a picture of their vehicles. These images are then processed to detect the license plate numbers and issue tickets accordingly.

Your task, in this homework, is to take an image of a license plate and programmatically (by writing a computer program) determine the license plate number. Each task in this homework will help you achieve this goal.

This homework needs the ImageWriter Library that can be downloaded from the notes on Image Processing on the course website. The ImageWriter library uses another library called “opencv” for image processing. The opencv library is installed in the cluster computers in rooms 1032, 2035, and 1185. If you use a personal computer, make sure that you install this library by following the instructions given on the image processing notes page.

Normalization

Before we can start processing a license plate, it is import for us to reduce the number of colors in the image. This process of color reduction is called normalization and we can do this by converting the image to black and white. This process helps us reduce the amount of information that we have to process. So the first step is to convert this colored image to a black and white image. We take each pixel of the image and if the average proportion of all three values: R, G and B is less than 100, we set the colors to 0 otherwise we set each component to 255.

You can use the following function in your code to convert a picture to black and white:

def convertBlackWhite(pic): rows = ImageWriter.getHeight(pic) columns = ImageWriter.getWidth(pic) for i in range(0,rows): for j in range(0,columns): c = ImageWriter.getColor(pic,j,i) if sum(c)//3 >= 100: ImageWriter.setColor(pic,j,i,[255,255,255]) else: ImageWriter.setColor(pic,j,i,[0,0,0]

Here is an image of a Qatari license plate without any processing

A regular Qatari license plate

After converting the image to Black&White, it should look similar to the following image

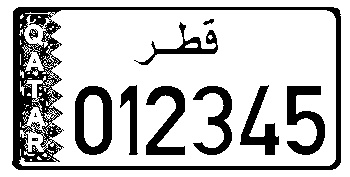
After converting the image to Black and White

Remove Border

The first thing we need to do with the black&white license plate is to remove the border around it. This allows us to reduce the amount of information that we will have to process. To remove the border, we start from the left side of the image. We observe that the left border is made up of contiguous black pixels and the first white pixel indicates the end of the border. This is a trivial observation but nonetheless important for our purposes. We take the image and start at the left most part of each row. Start by looking for the first black pixel.

Consider the following picture (zoomed in) of the top-left corner of a license plate:
Top left corner of the license plate

We start from the top row of the image and iterate horizontally through each column of this row and wait for the first black pixel. When we see the first black pixel, we set its value to white and after that every black pixel is changed to white until a white pixel is encountered. This white pixel would indicate the end of border. If we continue this process for the entire image, our results looks like the following:
License plate with border removed from left side

Notice that we still have the border on the right side leftover. This is because in the previous step, we started looking at the black pixel from left corner which ignored those black pixels that are on the right side. To remove this bit of pattern, we use a similar technique but start from the right side. So start looking at the pixels from the right most edge of the image and iterate backwards. The first contiguous set of black pixels should be converted to white. This results in the following:
Image of the license plate with borders removed

Task 1 Write a function called removeBorder(pic) that takes a picture as input and removes the border from the picture. The function should not return anything.

Remove Text on the Left

We notice in the last image of the previous section that we have some text on the left side that says Qatar. This needs to be removed for us to be able to locate the numbers on the license plate. Removing this text is similar to removing the border and we approach it in two steps: In the first step, we find out the location of the start and end of this blob of text. We use the following algorithm to do that:

# Find a vertical blob between # startRow and endRow Starting at inital Column initColumn x := initColumn hasBlack := False while x is less than the width of the image and hasBlack is False Repeat the following: go through each row from startRow to endRow If the current pixel is Black then this row has at least one black pixel, set hasBlack to True go to the next column by incrementing x by 1 #The previous column had a black pixel so save that location startX := x-1 #now we look for a column that is all white allWhite := False #go through all the rows again for each column while x is less than the width of the image and allWhite is False #assume that this is an all white line allWhite := True go through all the rows from startRow to endRow if the current color is black then this is not an all white column allWhite := False go on to the next column by incrementing x by 1 # At this point, # the previous column was an all white column # indicating the end of the text blob. endX := x-1 # At this point startX is the start of column of the blob # and endX is the end column of the blob.

Once we have found the start and end of the text, we need to set all the pixels there to White. We do that by calling a function that does that.

Task 2 Write a function called findVerticalBlob(pic,startRow, endRow, startColumn). This function returns startX and endX as a list as defined in the algorithm above.

Task 3 Write a function called removeColor(pic, startx, starty, endx, endy) that will set all pixels from rows starty to endy and columns startx to endx to white.

Calling the functions in the following order should clear out the text on the left as shown in the following figure.

columns = findVerticalBlob(pic,0,ImageWriter.getHeight(pic),0) removeColor(pic, columns[0],0,columns[1],ImageWriter.getHeight(pic))

Image of the license plate with borders and text removed

Horizontal Segmentation

Horizontal segmentation is the first main phase of locating the numerical characters on the license plate after all the surrounding noise has been reduced. First we will try to detect the starting row and ending row of the digits and hence the name horizontal segmentation. This involves writing an algorithm that will determine the location of imaginary red lines “start” and “end” shown here (note: the red lines are for illustration only):
Image of the license plate after Horizontal Segmentation (Red lines are only for illustration purpose)

This task is accomplished by treating any series of horizontal lines that have any black pixel as a “blob”. So, so let's start by looking at the following figure:
Image of the license plate with borders and text removed
If we start at the top of the image, there are a few horizontal lines that are all white. Then there is some text which is made up of a group of lines where each line has some black in it. This is followed by another small group of white lines and then some text and then a few empty rows. So in all we have two blobs on the image. If there is some noise in the image, then we might get more than three blobs. For example, consider the following figure:
License plate with some noisy data
The image in this figure will result in 4 blobs. One extra blob because of thin line at the top and one because of the line at the bottom.

Our goal is to find the biggest blob. The following algorithm outlines our methodology for finding the biggest horizontal blob.

#initialize variables inBlob := False startOfBlob := 0 maxBlob := 0 result := Empty List Loop through all rows of the image For this row, go through each column and check if there are any black pixels in this row If black pixels found and inBlob is False # This is start of a blob Set isBlob to True # save the start of blob Set startOfBlob to current row If no black pixels and inBlob is True Set inBlob to False Find size of the blob we just finished If size is bigger than biggest blob we have seen result = [startOfBlob,current row] maxBlob = size of this blob End Loop

Task 4 Write a function called horizontalSegmentation(pic). This function takes an image that does not have any borders as input argument. This function should determine the position of the numbers on the license plate and send the top and bottom of the area of license plate that holds the numbers. This information should be returned as a list of the format [top, bottom]

Vertical Segmentation

Once we have the numerical segments located, we will do the rest of the work with only this segment. Our task now is to figure out the location (start and end) of each of the digits in this vertical blob. For vertical segmentation, we start from the left most column of the image and step through each column. For each column we analyze each pixel in this column. In the beginning we will find that all pixels are white. As soon as we hit the first digit, the color will change to black. The first time we collect a black pixel we mark it the start of the digit and then keep on searching until we see a column that is all white. This would mark the end of this digit. We repeat this step six times, each time starting from the end of the last digit in order to search for the next digit. The function we wrote earlier, findVerticalBlob can do this task as long as we pass in the correct values of startRow, endRow, startColumn. In this case, startRow and endRow will be the limits we obtained from the horizontalSegmentation function and startColumn should be the end of the previous digit.

Decoding a Digit

Now that we have isolated each digit, recognizing each digit is a simple feature extraction and statistical analysis task. Feature extraction is just a fancy name for a simple process described below. Let’s take digit three as an example, we take this digit and divide it in four quadrants as shown:
Digit 3 divided into four quadrants

Now we calculate the percentage of black pixels in each quadrant of the digit. Percentage of black is taken by counting all black pixels in a quadrant and dividing it by the total number of pixels in the quadrant. We do this step for each of the four quadrants. Once we have these values for each quadrant, we compare with the measured value for each digit as shown in the table below. The values that match most closely is our prediction for this digit. Remember that just like in math, the top right quadrant is the first quadrant, the top left is the quadrant 2, and the rest follow counter clock-wise.

Digit Q1 Q2 Q3 Q4
0 0.49 0.51 0.52 0.48
1 0.72 0.34 0.005 0.69
2 0.54 0.30 0.51 0.34
3 0.50 0.24 0.22 0.47
4 0.16 0.28 0.41 0.52
5 0.35 0.69 0.32 0.46
6 0.41 0.64 0.54 0.52
7 0.59 0.32 0.37 0.08
8 0.54 0.54 0.51 0.51
9 0.53 0.54 0.39 0.62

We use statistical analysis for pixel matching. This is again a fancy word for the following algorithm. The table shows measured values for percentage of black pixels in each quadrant of each digit. For example, the fourth row in the table shows the percentages for digit 3. As can be seen from the figure of digit three above, and the table, there is a high number of black pixels in Quadrant 1, and the corresponding percentage is 50% in the table. Quadrant 3 has fewer black pixels and the corresponding percentage in Table 1 is 22%.

Also notice that several quadrants have very similar percentages for different digits. For example, in Quadrant 1, the percentage of digit 0 and 8 are very similar. Hence we have to use the knowledge of all four quadrants to determine the digits. We use the following statistical method: Let’s say we have a digit that we are trying to decode. We take this digit’s Q1 value, and subtract it from Q1 value for each digit. This shows us how close the two values are. If the difference is small, then the value are similar otherwise they are different. We divide this difference by 4 since we have four quadrants. We repeat this step for all four quadrants and add the results for each digit. The digit with the minimum overall difference most closely matches the sample digits and is our estimation for this digit.

Let's work an example. Assume that for a given digit, our values for Q1, Q2, Q3, and Q4 are 0.12, 0.28, 0.42, 0.54. Then for Digit 0, the absolute difference between corresponding quadrants is 0.37, 0.23, 0.1, 0.06, with a total difference equal to 0.37/4 + 0.23/4 + 0.1/4 + 0.06/4 = 0.19. Similarly, for Digit 4 we get values 0.04, 0.00, 0.01, 0.02 with an overall difference of 0.0175. When we get these overall difference values for all 10 digits, we can search for the smallest difference and that is our estimate for this particular digit.

Task 5 Write a function decodeCharacter(pic, startrow, endrow, startcol, endcol) that will take a pic as input parameter and decode the number bounded the rectangle represented by startrow, endrow, startcol, and endcol.

Putting it all together

Task 6 Write a function called decodeLicensePlate(filename) that will take a filename of a license plate image as input. The function should then load the image represented by filename and should return a string that represents the number on the license plate.

The decode license plate function should follow these steps: