CMUQ 15-121 More With Trees

• 1. Introduction
• 2. More Tree Vocabulary
  • 2.1. Full Binary Tree
  • 2.2. Complete Binary Tree
  • 2.3. Perfect Binary Tree
• 3. Another Way to Store Trees

1. Introduction

In this set of notes we’ll expand a on binary trees by giving some final terminology for them and discussing an alternative way to store them.

2. More Tree Vocabulary

Let’s look at three more vocabulary words related to binary trees.

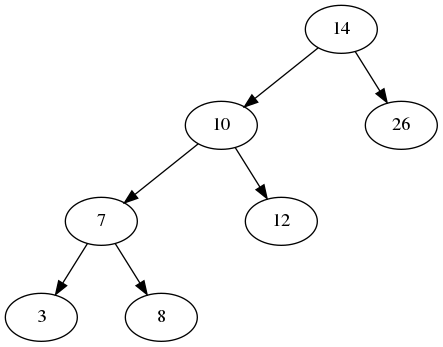
2.1. Full Binary Tree

A full binary tree is a tree where each node has exactly 0 or 2 children. Here is an example:

2.2. Complete Binary Tree

A complete binary tree is one where every level except the last one is completely filled, and the last level has all leaves as far left as possible. Here is an example:

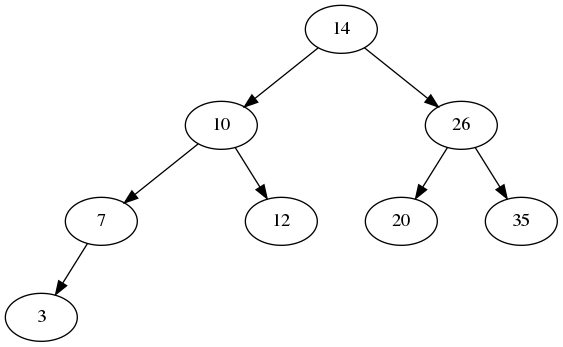
Notice that the example from the previous section (under full binary tree) is not a complete binary tree because the level containing 7 and 12 is not full.

2.3. Perfect Binary Tree

A perfect binary tree is like a complete binary tree where the last level is also full. Another way to define it is to say that all internal nodes have two children and all leaf nodes are at the same depth. Here is an example:

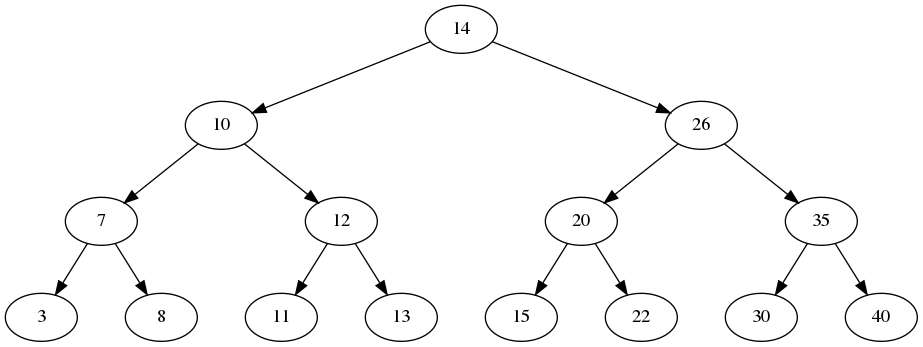
As an interesting side-note, all perfect trees are also full and complete.

3. Another Way to Store Trees

Consider the following binary tree:

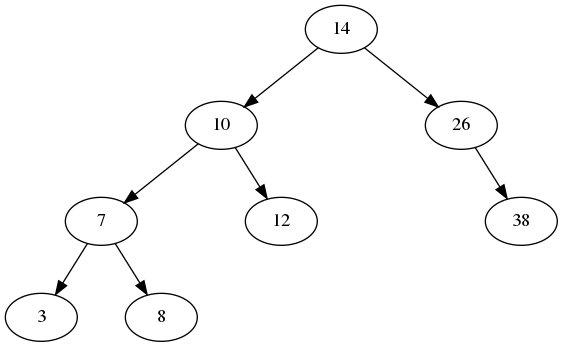
Thus far, we’ve stored binary trees by creating TreeNodes who each have a left and right pointer and forming the tree that way. However, there is an alternative way to store a binary tree using an array. Here is an array representation of that same tree:

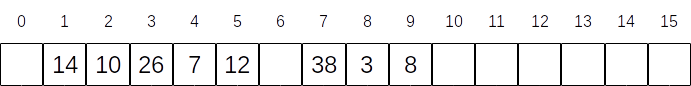
Notice the following properties:

• The root is stored at position 1.
• There is a spot in the array for every possible node in a perfect version of the tree.
  • For example, notice the empty space for the left child of 26 as well as all the missing children from the bottom of the tree.
• If a node is at location \(L\) in the tree, then its parent is at location \(\frac{L}{2}\). (Integer division.)
  • For example, considers nodes 3 and 8, who both have 7 as their parent. Node 3 is at location \(8\), and \(8/2=4\) so the parent is at 4. (Which is true.) Node 8 is at location \(9\), and \(9/2=4\), so the parent is at 4. (Which is also true.)

This is a valid way to store trees, and is actually simpler than storing pointers to nodes and such. The main downside of this approach, however, is wasted space. If a tree isn’t perfect, then there are empty spaces in the array.